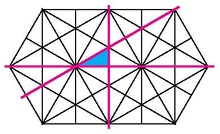
Coxeter-nedbrytningar av hyperboliska polygoner

En hyperbolisk triangel – dess inre vinklar summerar inte till 180 grader.

En Coxeter-nedbrytning av en polygon är en nedbrytning till ett ändligt antal polygoner där två som delar en sida är reflektioner av varandra längs den sidan. Hyperboliska polygoner är analogerna till euklidiska polygoner i hyperbolisk geometri . En hyperbolisk n -gon är ett område som begränsas av n segment, strålar eller hela räta linjer. Standardmodellen för denna geometri är skivmodellen Poincaré . En stor skillnad mellan euklidiska och hyperboliska polygoner är att summan av inre vinklar för en hyperbolisk polygon inte är samma som euklidiska polygoner. Speciellt är summan av vinklarna i en hyperbolisk triangel mindre än 180 grader.

En triangelgrupp som bildas genom att reflektera en triangel på dess sidor.

Coxeter-nedbrytningar är uppkallade efter Harold Scott MacDonald Coxeter , en fulländad 1900-talsgeometer. Han introducerade Coxeter-gruppen , en abstrakt grupp genererad av reflektioner. Dessa grupper har många användningsområden, inklusive att producera rotationer av platonska fasta ämnen och att tesselera planet.

Coxeter sönderfaller

Givet en polygon P kan en grupp G genereras genom att reflektera P runt dess sidor. Om vinklarna för P är π / k för naturliga tal k , så kommer G att vara diskret. En Coxeter-nedbrytning av en polygon är en nedbrytning till ett ändligt antal polygoner där två som delar en sida är reflektioner av varandra längs den sidan.

Målet med en Coxeter-nedbrytning är att bryta upp en polygon i en sammansättning av kongruenta trianglar som reflekteras på dess sidor.

Hyperboliska trianglar

Om triangeln ABC kan genomgå Coxeter-nedbrytning och har vinklar ${\displaystyle k_{i}{\frac {\pi }{q_{i}}}} ,$ där $k_{i}$ är antalet gånger ${\displaystyle i}:$ e vinkeln bryts upp kan triangeln ABC skrivas som $\left({\frac { k_{1}}{q_{1}}},{\frac {k_{2}}{q_{2}}},{\frac {k_{3}}{q_{3}}}\right)$ . Flera egenskaper hos dessa fundamentala polygoner är kända för hyperboliska trianglar.

Nedbrytningen av en triangel med tre fundamentala vinklar

• Grundtriangeln har en rät vinkel. Beviset för detta involverar två fall beroende på om vinklarna för den sönderdelade triangeln är fundamentala. Om de inte är det, följer det att eftersom nedbrytningsprocessen är ändlig, kommer så småningom en fundamental triangel att bildas med en rät vinkel. Om de är det, bevisar ett motsägelsebevis baserat på arean av den fundamentala triangeln att den kommer att ha en rät vinkel.
• För en triangel ${\displaystyle \left({\frac {k_{1}}{q_{1}}},{\frac {k_{2} }{q_{2}}},{\frac {k_{3}}{q_{3}}}\right)} ,$ minst två $q_{i}$ är lika. Detta bevisas också genom motsägelse baserat på arean av den fundamentala polygonen som hittas med Gauss-Bonnet-satsen . Vi kan säga att arean av hela triangeln är lika med antalet fundamentala trianglar gånger deras area. Detta ger oss $1-\summa _{i=1}^{3}{\frac {k_ {i}}{q_{i}}}=N\left(1-\summa _{i=1}^{3}{\frac {1}{q_{i}}}\right)$ . Om vi ​​antar att $q_{1}>q_{2}>q_{3}$ så bryts den tidigare likheten för $N>1$ . Därför är minst två vinklar lika.
• Givet en triangel där alla tre vinklarna är fundamentala, finns det en enda sönderdelning. Ett icke-trivialt bevis på detta finns i.
• Alla möjliga sönderdelningar är kända.
  

  Dessa är alla Coxeter-nedbrytningar av hyperboliska trianglar, exklusive den mer detaljerade ovan.

Andra hyperboliska polygoner

Fyrhörningar kan också ha Coxeter-nedbrytningar.

• Om en fyrhörning inte är konvex, finns det två möjliga triangulära sönderdelningar. Detta görs genom att sönderdela den i två trianglar och sedan sönderdela dessa. Dessa två trianglar är trubbiga.
• En fyrhörning kan brytas ner av fyrhörningar.
• Alla nedbrytningar av konvexa fyrhörningar är också kända. Att visa dem alla är opraktiskt i den här artikeln, men några är avbildade här.
  

  Nedbrytningarna för icke-konvexa fyrhörningar.
  

  Nedbrytningar av fyrhörningar till fyrhörningar

Några av nedbrytningarna av fyrhörningar