Confluence (abstrakt omskrivning)

Inom datavetenskap är konfluens en egenskap hos att skriva om system, som beskriver vilka termer i ett sådant system som kan skrivas om på mer än ett sätt, för att ge samma resultat. Den här artikeln beskriver egenskaperna i den mest abstrakta miljön för ett abstrakt omskrivningssystem .
Motiverande exempel
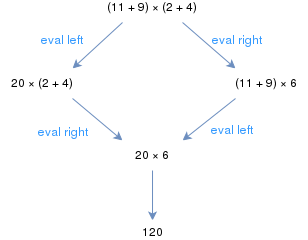
De vanliga reglerna för elementär aritmetik bildar ett abstrakt omskrivningssystem. Till exempel kan uttrycket (11 + 9) × (2 + 4) utvärderas med början antingen till vänster eller höger parentes; i båda fallen erhålls dock till slut samma resultat. Om varje aritmetiskt uttryck utvärderas till samma resultat oavsett reduktionsstrategi, sägs det aritmetiska omskrivningssystemet vara markkonfluent. Aritmetiska omskrivningssystem kan vara sammanflytande eller endast marksammanflytande beroende på detaljer i omskrivningssystemet.
Ett andra, mer abstrakt exempel erhålls från följande bevis på att varje gruppelement är lika med inversen av dess invers:
| A1 | 1 ⋅ a | = a |
| A2 | a −1 ⋅ a | = 1 |
| A3 | ( a ⋅ b ) ⋅ c | = a ⋅ ( b ⋅ c ) |
| a −1 ⋅ ( a ⋅ b ) | ||
| = | ( a −1 ⋅ a ) ⋅ b | av A3(r) |
| = | 1 ⋅ b | av A2 |
| = | b | av A1 |
| ( a −1 ) −1 ⋅ 1 | ||
| = | ( a −1 ) −1 ⋅ ( a −1 ⋅ a ) | av A2(r) |
| = | a | av R4 |
| ( a −1 ) −1 ⋅ b | ||
| = | ( a −1 ) −1 ⋅ ( a −1 ⋅ ( a ⋅ b )) | av R4(r) |
| = | a ⋅ b | av R4 |
| a ⋅ 1 | ||
| = | ( a −1 ) −1 ⋅ 1 | av R10(r) |
| = | a | av R6 |
| ( a −1 ) −1 | ||
| = | ( a −1 ) −1 ⋅ 1 | av R11(r) |
| = | a | av R6 |
Detta bevis utgår från de givna gruppaxiomen A1–A3 och fastställer fem satser R4, R6, R10, R11 och R12, var och en av dem använder några tidigare, och R12 är huvudsatsen. Vissa av bevisen kräver icke-uppenbara, eller till och med kreativa, steg, som att tillämpa axiom A2 omvänt, och därigenom skriva om "1" till " a −1 ⋅ a" i det första steget av R6:s bevis. En av de historiska motiven för att utveckla teorin om termomskrivning var att undvika behovet av sådana steg, som är svåra att hitta av en oerfaren människa, än mindre av ett datorprogram.
Om ett termomskrivningssystem är sammanflytande och avslutande , finns det en enkel metod för att bevisa likhet mellan två uttryck (även känd som termer ) s och t : Börja med s , tillämpa likheter från vänster till höger så länge som möjligt, för att så småningom få en term s " . Erhåll från t en term t′ på liknande sätt. Om båda termerna s′ och t′ bokstavligen överensstämmer, är s och t (inte överraskande) bevisat lika. Ännu viktigare, om de inte håller med, s och t inte vara lika. Det vill säga att alla två termer s och t som överhuvudtaget kan bevisas vara lika kan göras med den metoden.
Framgången för den metoden beror inte på en viss sofistikerad ordning för att tillämpa omskrivningsregler, eftersom sammanflöde säkerställer att varje sekvens av regelapplikationer så småningom kommer att leda till samma resultat (medan termineringsegenskapen säkerställer att alla sekvenser så småningom når ett slut alls). Därför, om ett sammanflytande och avslutande termomskrivningssystem kan tillhandahållas för någon ekvationsteori , krävs det inte ett streck av kreativitet för att utföra bevis på termens likhet; den uppgiften blir därmed mottaglig för datorprogram. Moderna metoder hanterar mer generella abstrakta omskrivningssystem snarare än termomskrivningssystem ; de senare är ett specialfall av de förra.
Allmänt fall och teori
Ett omskrivningssystem kan uttryckas som en riktad graf där noder representerar uttryck och kanter representerar omskrivningar. Så, till exempel, om uttrycket a kan skrivas om till b , då säger vi att b är en reduktion av a (alternativt reduceras a till b , eller a är en expansion av b ). Detta representeras med pilnotation; a → b anger att a reduceras till b . Intuitivt betyder detta att motsvarande graf har en riktad kant från a till b .
Om det finns en väg mellan två grafnoder c och d , bildar den en reduktionssekvens . Så, till exempel, om c → c′ → c′′ → ... → d′ → d , så kan vi skriva c d , vilket indikerar förekomsten av en reduktionssekvens från c till d . Formellt den reflexiv-transitiva stängningen av →. Med exemplet från föregående stycke har vi (11+9)×(2+4) → 20×(2+4) och 20×(2+4) → 20×6, så (11+9)×( 2+4) 20×6.
Med detta fastställt kan sammanflöde definieras enligt följande. a ∈ S anses sammanflytande om det för alla par b , c ∈ S så att a b och a c finns ett d ∈ S med b d och c d (betecknas ). Om varje a ∈ S är konfluent, säger vi att → är konfluent. Denna egenskap kallas ibland även diamantegenskapen , efter formen på diagrammet som visas till höger. Vissa författare reserverar termen diamantegenskap för en variant av diagrammet med enstaka reduktioner överallt; det vill säga närhelst a → b och a → c måste det finnas ett d så att b → d och c → d . Enkelreduktionsvarianten är strikt starkare än multireduktionsvarianten.
Marksammanflöde
Ett termomskrivningssystem är jordkonfluent om varje grundterm är konfluent, det vill säga varje term utan variabler.
Lokalt sammanflöde
Ett element a ∈ S sägs vara lokalt (eller svagt) konfluent om det för alla b , c ∈ S med a → b och a → c finns d ∈ S med b d och c d . Om varje a ∈ S är lokalt sammanflytande, kallas → lokalt (eller svagt) sammanflytande, eller har den svaga egenskapen Church–Rosser . Detta skiljer sig från sammanflödet genom att b och c måste reduceras från a i ett steg. I analogi med detta, kallas sammanflöde ibland som globalt sammanflöde .
Relationen , införd som en notation för reduktionssekvenser, kan ses som ett omskrivningssystem i sin egen rätt, vars relation är den reflexiv-transitiva stängningen av → . Eftersom en sekvens av reduktionssekvenser återigen är en reduktionssekvens (eller, ekvivalent, eftersom att bilda den reflexiv-transitiva förslutningen är idempotent ), = . Det följer att → är sammanflytande om och endast om är lokalt sammanflytande.
Ett omskrivningssystem kan vara lokalt sammanflytande utan att vara (globalt) sammanflytande. Exempel visas i bild 3 och 4. Newmans lemma säger dock att om ett lokalt sammanflytande omskrivningssystem inte har några oändliga reduktionssekvenser (i vilket fall det sägs vara avslutande eller starkt normaliserande ), så är det globalt sammanflytande.
Kyrka–Rosser egendom
Ett omskrivningssystem sägs ha egenskapen Church–Rosser om och endast om innebär för alla objekt x , y . Alonzo Church och J. Barkley Rosser bevisade 1936 att lambdakalkyl har denna egenskap; därav namnet på fastigheten. (Det faktum att lambdakalkyl har denna egenskap kallas också för Church–Rosser-satsen .) I ett omskrivningssystem med egenskapen Church–Rosser kan ordproblemet reduceras till sökandet efter en gemensam efterträdare. I ett Church–Rosser-system har ett objekt högst en normalform ; det vill säga att den normala formen av ett objekt är unik om det finns, men det kanske inte existerar. I lambdakalkyl till exempel har uttrycket (λx.xx)(λx.xx) inte en normal form eftersom det finns en oändlig sekvens av β-reduktioner (λx.xx)(λx.xx) → (λx.xx) (λx.xx) → ...
Ett omskrivningssystem besitter egenskapen Church–Rosser om och endast om den är sammanflytande. På grund av denna likvärdighet påträffas en hel del variation i definitioner i litteraturen. Till exempel, i "Terese" definieras Church–Rossers egendom och sammanflöde som synonyma och identiska med definitionen av sammanflöde som presenteras här; Church–Rosser som definieras här förblir namnlös, men ges som en likvärdig egenskap; detta avsteg från andra texter är medvetet.
Semikonfluens
Definitionen av lokalt sammanflöde skiljer sig från det för globalt sammanflöde genom att endast element som nås från ett givet element i ett enda omskrivningssteg beaktas. Genom att betrakta ett element som nås i ett enda steg och ett annat element nått av en godtycklig sekvens kommer vi fram till det mellanliggande begreppet semi-konfluens: a ∈ S sägs vara semi-konfluent om för alla b , c ∈ S med a → b och a c finns d ∈ S med b d och c d ; om varje a ∈ S är semi-konfluent, säger vi att → är semi-konfluent.
Ett semi-konfluent element behöver inte vara konfluent, men ett semi-konfluent omskrivningssystem är nödvändigtvis konfluent, och ett konfluent system är trivialt semi-konfluent.
Starkt sammanflöde
Stark konfluens är en annan variant av lokal sammanflytning som låter oss dra slutsatsen att ett omskrivningssystem är globalt sammanflytande. Ett element a ∈ S sägs vara starkt konfluent om det för alla b , c ∈ S med a → b och a → c finns d ∈ S med b d och antingen c → d eller c = d ; om varje a ∈ S är starkt konfluent, säger vi att → är starkt konfluent.
Ett sammanflytande element behöver inte vara starkt sammanflytande, men ett starkt sammanflytande omskrivningssystem är nödvändigtvis sammanflytande.
Exempel på sammanflytande system
- Reduktion av polynom modulo an ideal är ett konfluent omskrivningssystem förutsatt att man arbetar med Gröbner-bas .
- Matsumotos sats följer av sammanflödet av flätförhållandena.
- β-reduktion av λ-termer sammanfaller med Church–Rosser-satsen .
Se även
Anteckningar
- Term Rewriting Systems , Terese, Cambridge Tracts in Theoretical Computer Science, 2003.
- Term Rewriting and All That , Franz Baader och Tobias Nipkow , Cambridge University Press, 1998