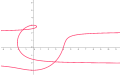
Conchoid av Dürer

Conchoid av Dürer, konstruerad av honom själv

Inom geometrin är Dürers conchoid , även kallad Dürers skalkurva , en plan , algebraisk kurva , uppkallad efter Albrecht Dürer och introducerad 1525. Det är inte en riktig conchoid .

Konstruktion

Konstruktion av Dürers conchoid

Antag att två vinkelräta linjer ges, med skärningspunkten O . För konkrethetens skull kan vi anta att dessa är koordinataxlarna och att O är ursprunget, det vill säga (0, 0). Låt punkterna $Q = (q, 0)$ och $R = (0, r)$ röra sig på axlarna på ett sådant sätt att $q + r = b$ , en konstant. Markera punkterna $P$ och $P'$ på linjen $QR , förlängd vid behov,$ på ett fast avstånd $a$ från $Q$ . Platsen för punkterna $P$ och $P'$ är Dürers conchoid.

Ekvation

Konchoidens ekvation i kartesisk form är

2y^{2}(x^{2}+y^{2})-2by^{2}(x+y)+(b^{2}-3a ^{2})y^{2}-a^{2}x^{2}+2a^{2}b(x+y)+a^{2}(a^{2}-b^{2} })=0.

I parametrisk form ges ekvationen av

{\begin{aligned}x&={\frac {b\cos(t)}{\cos(t)-\sin(t)}}+a\cos(t),\\y&=a\sin(t),\end{aligned}}

där parametern $t$ mäts i radianer .

Egenskaper

Kurvan har två komponenter, asymptotisk till linjerna $y=\pm a/{\sqrt {2}}$ . Varje komponent är en rationell kurva . Om a > b finns det en slinga, om a = b finns det en spets vid (0, a ).

Särskilda fall inkluderar:

a = 0: linjen y = 0;
b = 0: linjeparet $y=\pm a/{\sqrt {2}}$ tillsammans med cirkeln $x^{2} +y^{2}=a^{2}$ ;

a = 3, b = 1, slingan visas
a = 3, b = 3, spets visas
a = 3, b = 5

Enveloppen av räta linjer som används i konstruktionen bildar en parabel (som ses i Durers ursprungliga diagram ovan) och därför är kurvan en punktglissett som bildas av en linje och en av dess punkter som glider mot en parabel respektive en av dess tangenter.

Historia

Den beskrevs först av den tyske målaren och matematikern Albrecht Dürer (1471–1528) i hans bok Underweysung der Messung ( Instruktion i mätning med kompass och rak s. 38), och kallar den Ein muschellini ( Conchoid or Shell ). Dürer ritade bara en gren av kurvan.

Se även

externa länkar

Weisstein, Eric W. "Dürers Conchoid" . MathWorld .