Centralt differensschema

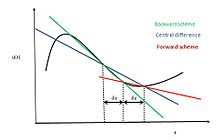
Figur 1. Jämförelse av olika scheman

I tillämpad matematik är det centrala differentieringsschemat en ändlig skillnadsmetod som optimerar approximationen för differentialoperatorn i den centrala noden av den betraktade patchen och tillhandahåller numeriska lösningar på differentialekvationer. Det är ett av scheman som används för att lösa den integrerade konvektion-diffusionsekvationen och för att beräkna den transporterade egenskapen Φ vid e- och w-ytorna, där e och w är förkortningar för öst och väst (kompassriktningar används vanligtvis för att indikera riktningar på beräkningsteknik rutnät). Metodens fördelar är att den är lätt att förstå och implementera, åtminstone för enkla materiella relationer; och att dess konvergenshastighet är snabbare än vissa andra finita differensmetoder, såsom särskiljning framåt och bakåt. Den högra sidan av konvektions-diffusionsekvationen, som i grunden belyser diffusionstermerna, kan representeras med hjälp av central skillnadsapproximation. För att förenkla lösningen och analysen kan linjär interpolation användas logiskt för att beräkna cellernas nominella värden för den vänstra sidan av denna ekvation, som inte är något annat än de konvektiva termerna. Därför kan cellernas nominella värden för egendom för ett enhetligt rutnät skrivas som:

\Phi _{e}=(\Phi _{P}+\Phi _{E})/2

\Phi _{w}=(\Phi _{W}+\Phi _{P})/2

Steady-state konvektionsdiffusionsekvation

Konvektion -diffusionsekvationen är en kollektiv representation av diffusions- och konvektionsekvationer, och beskriver eller förklarar alla fysiska fenomen som involverar konvektion och diffusion i överföringen av partiklar, energi och andra fysiska storheter inuti ett fysiskt system:

\operatörsnamn {div} (\rho u\varphi )=\operatörsnamn {div} (\Gamma \nabla \varphi )+S_{\varphi };\,

...där Г är diffusionskoefficient och Φ är egenskapen .

Formulering av konstant konvektionsdiffusionsekvation

Formell integrering av konvektion-diffusionsekvationen i konstant tillstånd över en kontrollvolym ger

\int \limits _{A}\,n\cdot (\rho u\varphi )\,dA=\int \limits _{A}\,n\cdot (\Gamma \nabla \varphi )\,dA+\int \limits _{CV}\,S_{\varphi }\,dV

→ Ekvation 1.

Denna ekvation representerar flödesbalans i en kontrollvolym. Den vänstra sidan ger nettokonvektionsflödet, och den högra sidan innehåller nettodiffusionsflödet och genereringen eller förstörelsen av egenskapen inom kontrollvolymen.

I avsaknad av källtermekvation blir man

{d \over dx}(\rho u\varphi )={d \over dx}\left({d\varphi \over dx}\right)

→ Ekvation 2.

Kontinuitetsekvation :

{d \over dx}(\rho u)=0

→ Ekvation 3.

Figur 2. Interpolationsmetod

Att anta en kontrollvolym och integrera ekvation 2 över kontrollvolymen ger:

{\displaystyle (\rho u\varphi A)_{ e}-(\rho u\varphi A)_{w}=(\Gamma Ad\varphi /dx)_{e}-(\Gamma Ad\varphi /dx)_{w}} → Integrerad konvektion

- diffusionsekvation

Integration av ekvation 3 ger:

(\rho uA)_{e}-(\rho uA)_{w}=0

→ Integrerad kontinuitetsekvation

Det är bekvämt att definiera två variabler för att representera det konvektiva massflödet per ytenhet och diffusionskonduktans vid cellytor, till exempel:

F=\rho u

D=\Gamma /\delta x

Om vi antar $A_{e}=A_{w}$ kan vi skriva integrerad konvektion-diffusionsekvation som:

F_{e}\varphi _{e}-F_{w}\varphi _ {w}=D_{e}(\varphi _{E}-\varphi _{P})-D_{w}(\varphi _{P}-\varphi _{W})

Och integrerad kontinuitetsekvation som:

F_{e}-F_{w}=0

I ett centralt differensschema försöker vi linjär interpolation för att beräkna cellnosvärden för konvektionstermer.

För ett enhetligt rutnät kan vi skriva cellnosvärden för egenskapen Φ as

\varphi _{e}=(\varphi _{E}+\varphi _{P}) /2,\quad \varphi _{w}=(\varphi _{P}+\varphi _{W})/2

När vi ersätter detta med en integrerad konvektionsdiffusionsekvation får vi:

F_{e}{\frac {\varphi _{E}+\varphi _{P}}{2}}-F_{w}{\frac {\varphi _{W}+\varphi _{P}}{2}}=D_{e}(\ varphi _{E}-\varphi _{P})-D_{w}(\varphi _{P}-\varphi _{W})

Och på att arrangera om:

\left[\left(D_{w}+{\frac {F_{w}}{2}}\right)+\left(D_{e}-{\frac {F_{e}}{ 2}}\right)+(F_{e}-F_{w})\right]\varphi _{P}=\left(D_{w}+{\frac {F_{w}}{2}}\ höger)\varphi _{W}+\left(D_{e}-{\frac {F_{e}}{2}}\right)\varphi _{E}

$a_{P}\varphi _{P}=a_{W}\varphi _{W}+a_{E}\varphi _{E}$

Olika aspekter av centralt differensschema

Konservativitet

Bevarande säkerställs i centralt differensschema eftersom den totala flödesbalansen erhålls genom att summera nettoflödet genom varje kontrollvolym med hänsyn till gränsflödena för kontrollvolymerna runt nod 1 och 4.

Figur 3. Typisk illustration

Gränsflöde för kontrollvolym runt nod 1 och 4

{\begin{aligned}&\left[{\frac {\Gamma _{e_{1}}(\varphi _{2}-\varphi _{1})}{\delta x}}-q_{A} \right]+\left[{\frac {\Gamma _{e_{2}}(\varphi _{3}-\varphi _{2})}{\delta x}}-{\frac {\Gamma _ {w_{2}}(\varphi _{2}-\varphi _{1})}{\delta x}}\right]\\[10pt]+{}&\left[{\frac {\Gamma _ {e_{3}}(\varphi _{4}-\varphi _{3})}{\delta x}}-{\frac {\Gamma _{w_{3}}(\varphi _{3}- \varphi _{2})}{\delta x}}\right]+\left[q_{B}-{\frac {\Gamma _{w_{4}}(\varphi _{4}-\varphi _ {3})}{\delta x}}\right]=q_{B}-q_{A}\end{aligned}}

eftersom $\Gamma _{e_{1}}=\Gamma _{w_{2}},\Gamma _ {e_{2}}=\Gamma _{w_{3}},\Gamma _{e_{3}}=\Gamma _{w_{4}}$

Begränsadhet

Centralt differensschema uppfyller det första villkoret för begränsning .

Eftersom $F_{e}-F_{w}=0$ från kontinuitetsekvationen, därför; $a_{P}\varphi _{P}=a_{W}\varphi _{W}+a_{E}\varphi _{E}$

Ett annat väsentligt krav för begränsning är att alla koefficienter i de diskretiserade ekvationerna ska ha samma tecken (vanligtvis alla positiva). Men detta är bara uppfyllt när ( pecletnummer ) $F_{e}/D_{e}<2$ eftersom för ett enkelriktat flöde ( $F_{ e}>0,F_{w}>0$ ) $a_{E}=(D_{e}-F_{e}/2)$ är alltid positiv om $D_{e}>F_{e}/2$

Transportivitet

Det kräver att transportiviteten ändras enligt storleken på peklettalet, dvs när pe är noll $\varphi$ sprids i alla riktningar lika och när Pe ökar (konvektion > diffusion) beror $\varphi$ vid en punkt till stor del på uppströmsvärde och mindre på nedströmsvärde. Men centralt differentieringsschema har inte transportivitet vid högre pe eftersom Φ vid en punkt är genomsnittet av närliggande noder för alla Pe.

Noggrannhet

Taylor -seriens trunkeringsfel för det centrala differensschemat är andra ordningens. Centralt differensschema kommer endast att vara korrekt om Pe < 2. På grund av denna begränsning är central differens inte en lämplig diskretiseringspraxis för generella flödesberäkningar.

Tillämpningar av centrala differenssystem

De används för närvarande regelbundet i lösningen av Euler-ekvationerna och Navier–Stokes-ekvationerna .
Resultat som använder central differentieringsapproximation har visat märkbara förbättringar i noggrannhet i släta områden.
Stötvågsrepresentation och gränsskiktsdefinition kan förbättras på grova maskor.

Fördelar

Enklare att programmera, kräver mindre datortid per steg och fungerar bra med multigrid - accelerationstekniker
Har en fri parameter i samband med den fjärde differensförlusten, som behövs för att närma sig ett stabilt tillstånd.
Mer exakt än första ordningens uppvindsschema om Peclet-talet är mindre än 2.

Nackdelar

Något mer försvinnande
Leder till oscillationer i lösningen eller divergens om det lokala Peclet-talet är större än 2.

Se även

Vidare läsning

Computational Fluid Dynamics: The Basics with Applications – John D. Anderson, ISBN 0-07-001685-2
Computational Fluid Dynamics volym 1 – Klaus A. Hoffmann, Steve T. Chiang, ISBN 0-9623731-0-9

externa länkar