Blockera cellulär automat
En cellulär blockautomat eller partitioneringscellautomat är en speciell typ av cellulär automat där cellnätet är uppdelat i icke-överlappande block (med olika partitioner vid olika tidssteg) och övergångsregeln tillämpas på ett helt block åt gången snarare än en enda cell. Cellulära blockautomater är användbara för simuleringar av fysiska kvantiteter, eftersom det är enkelt att välja övergångsregler som följer fysiska begränsningar som reversibilitet och bevarandelagar .
Definition
En blockcellulär automat består av följande komponenter:
- Ett vanligt gitter av celler
- En ändlig uppsättning av tillstånden som varje cell kan vara i
- En uppdelning av cellerna i en enhetlig tessellation där varje bricka på partitionen har samma storlek och form
- En regel för att flytta partitionen efter varje tidssteg
- En övergångsregel, en funktion som tar som indata en tilldelning av tillstånd för cellerna i en enskild bricka och producerar som utdata ytterligare en tilldelning av tillstånd för samma celler.
I varje tidssteg tillämpas övergångsregeln samtidigt och synkront på alla brickor i partitionen. Sedan flyttas partitionen och samma operation upprepas i nästa tidssteg och så vidare. På detta sätt, som med vilken cellulär automat som helst, ändras mönstret av celltillstånd över tiden för att utföra någon icke-trivial beräkning eller simulering.
Grannskap
Det enklaste uppdelningsschemat är förmodligen Margolus-kvarteret , uppkallat efter Norman Margolus , som först studerade blockcellulära automater med denna grannskapsstruktur. I området Margolus är gittret uppdelat i 2 -cellsblock (eller 2 × 2 kvadrater i två dimensioner, eller 2 × 2 × 2 kuber i tre dimensioner, etc.) som förskjuts med en cell (längs varje dimension) på alternativa tidssteg.
En närbesläktad teknik på grund av K. Morita och M. Harao består i att dela upp varje cell i ett ändligt antal delar, där varje del ägnas åt någon granne. Utvecklingen fortskrider genom att byta ut motsvarande delar mellan grannar och sedan applicera på varje cell en rent lokal transformation endast beroende på cellens tillstånd (och inte på dess grannars tillstånd). Med ett sådant konstruktionsschema är den cellulära automaten garanterat reversibel om den lokala transformationen i sig är en bijektion . Denna teknik kan ses som en blockcellulär automat på ett finare gitter av celler, bildat av delarna av varje större cell; blocken i detta finare gitter växlar mellan uppsättningarna av delar inom en enda stor cell och uppsättningarna av delar i närliggande celler som delar delar med varandra.
Reversibilitet och bevarande
Så länge regeln för att utveckla varje block är reversibel , kommer hela automaten också att vara det. Starkare, i detta fall kan automatens tidsomvända beteende också beskrivas som en blockcellulär automat, med samma blockstruktur och med en övergångsregel som inverterar den ursprungliga automatens regel inom varje block. Det omvända är också sant: om blocken inte är individuellt reversibla kan den globala utvecklingen inte vara reversibel: om två olika konfigurationer x och y av ett block leder till samma resultattillstånd z , då skulle en global konfiguration med x i ett block vara omöjlig att skilja efter ett steg från konfigurationen där x ersätts med y . Det vill säga, en cellulär automat är reversibel globalt om och endast om den är reversibel på blocknivå.
Lättheten att designa reversibla cellulära blockautomater och att testa blockcellulära automater för reversibilitet står i stark kontrast till cellulära automater med andra icke-blockbaserade grannskapsstrukturer, för vilka det är oklart om automaten är reversibel och för vilken den omvända dynamiken kan kräver mycket större stadsdelar än framåtdynamiken. Vilken som helst reversibel cellulär automat kan simuleras av en reversibel cellulär blockautomat med ett större antal tillstånd; på grund av den obestämbara reversibiliteten för icke-blockerade cellulära automater, finns det dock ingen beräkningsbar gräns på radien för regionerna i den icke-blockerade automaten som motsvarar block i simuleringen, och översättningen från en icke-blockerande regel till en blockregel är inte heller beräkningsbar.
Cellulära blockautomater är också en bekväm formalism för att utforma regler som, förutom reversibilitet, implementerar bevarandelagar såsom bevarande av partikelantal, bevarande av rörelsemängd, etc.. Till exempel, om regeln inom varje block bevarar numret av levande celler i blocket, kommer den globala utvecklingen av automaten också att bevara samma antal. Denna egenskap är användbar vid tillämpningar av cellulära automater för fysisk simulering.
Simulering med konventionella cellulära automater
Som Toffoli och Margolus skriver, introducerar inte blockcellsautomatmodellen någon ytterligare kraft jämfört med en konventionell cellulär automat som använder samma grannskapsstruktur vid varje tidssteg: vilken cellulär blockautomat som helst kan simuleras på en konventionell cellulär automat genom att använda fler tillstånd och ett större kvarter. Närmare bestämt, låt de två automaterna använda samma gitter av celler, men låt varje tillstånd hos den konventionella automaten specificera tillståndet för blockautomaten, fasen för dess partitionsskiftningsmönster och cellens position inom dess block. Till exempel, med Margolus-kvarteret, skulle detta öka antalet tillstånd med en faktor åtta: det finns fyra möjliga positioner som en cell kan ta i sitt 2 × 2- block, och två faser till partitionen. Låt dessutom den konventionella automatens grannskap vara föreningen av blocken som innehåller den givna cellen i den cellulära blockautomaten. Med denna grannskaps- och tillståndsstruktur kan sedan varje uppdatering av blockautomaten simuleras av en enda uppdatering av den konventionella cellulära automaten.
Ansökningar
Cellulära blockautomater används vanligtvis för att implementera gittergaser och andra kvasifysiska simuleringar, på grund av att det är lätt att simulera fysiska begränsningar såsom bevarandelagar i dessa system. Till exempel kan Margolus-modellen användas för att simulera HPP-gittergasmodellen, där partiklar rör sig i två vinkelräta riktningar och sprids i rät vinkel när de kolliderar med varandra. I den cellulära blocksimuleringen av denna modell flyttar uppdateringsregeln varje cell till cellen diagonalt motsatt i sitt block, förutom i det fall att en cell innehåller två diagonalt motsatta partiklar, i vilket fall de ersätts av det komplementära paret av diagonalt motsatta partiklar. På så sätt rör sig partiklar diagonalt och sprids enligt HPP-modellen. En alternativ regel som simulerar HPP-gittergasmodellen med horisontell och vertikal rörelse av partiklar, snarare än med diagonal rörelse, involverar att rotera innehållet i varje block medurs eller moturs i alternerande faser, utom igen i det fall att en cell innehåller två diagonalt motsatta partiklar, i vilket fall det förblir oförändrat. I någon av dessa modeller är momentum (summan av hastighetsvektorerna för de rörliga partiklarna) bevarat, såväl som deras antal, en väsentlig egenskap för att simulera fysikaliska gaser. HPP-modellerna är dock något orealistiska som en modell av gasdynamik, eftersom de har ytterligare icke-fysiska bevaranderegler: den totala rörelsemängden inom varje rörelselinje, såväl som den totala rörelsemängden för det övergripande systemet, bevaras. Mer komplexa modeller baserade på det hexagonala rutnätet undviker detta problem.
Dessa automater kan också användas för att modellera rörelsen av sandkorn i sandhögar och timglas . I den här applikationen kan man använda ett Margolus-kvarter med en uppdateringsregel som bevarar antalet korn inom varje 2 × 2- block men som flyttar varje korn så långt ner inom sitt block som möjligt. Om ett block innehåller två korn som är staplade vertikalt ovanpå varandra, ersätter automatens övergångsfunktion det med ett block där kornen ligger sida vid sida, vilket i själva verket tillåter höga sandhögar att välta och spridas. Denna modell är inte reversibel, men den följer fortfarande en bevarandelag om antalet partiklar. En modifierad regel, som använder samma grannskap men flyttar partiklarna i sidled i den utsträckning det är möjligt såväl som nedåt, tillåter de simulerade sandhögarna att spridas även när de inte är särskilt branta. Mer sofistikerade sandpålar med cellulära automater är också möjliga, med fenomen som vindtransport och friktion.
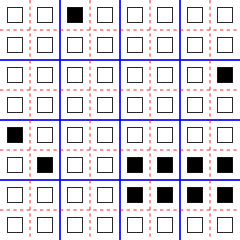
Margolus ursprungliga applikation för den blockcellulära automatmodellen var att simulera biljardbollsmodellen för reversibel beräkning, där booleska logiska signaler simuleras av rörliga partiklar och logiska grindar simuleras av elastiska kollisioner av dessa partiklar. Det är till exempel möjligt att utföra biljardbollsberäkningar i den tvådimensionella Margolus-modellen, med två tillstånd per cell och med antalet levande celler som bevaras av modellens utveckling. I "BBM"-regeln som simulerar biljardbollsmodellen på detta sätt består signalerna av enstaka levande celler som rör sig diagonalt. För att åstadkomma denna rörelse ersätter blockövergångsfunktionen ett block som innehåller en enda levande cell med ett annat block där cellen har flyttats till blockets motsatta hörn. På liknande sätt kan elastiska kollisioner utföras av en blockövergångsfunktion som ersätter två diagonalt motsatta levande celler med de andra två cellerna i blocket. I alla andra konfigurationer av ett block gör blockövergångsfunktionen ingen förändring av dess tillstånd. I denna modell 2 × 4 rektanglar av levande celler (noggrant inriktade med avseende på partitionen) stabila och kan användas som speglar för att styra de rörliga partiklarnas vägar. Till exempel visar illustrationen av området Margolus fyra partiklar och en spegel; om nästa steg använder den blå partitionen, så rör sig två partiklar mot spegeln medan de andra två är på väg att kollidera, medan om nästa steg använder den röda partitionen, så rör sig två partiklar bort från spegeln och de andra två har precis kolliderade och kommer att flytta isär från varandra.
Ytterligare regler
Toffoli och Margolus föreslår ytterligare två reversibla regler för Margolus-kvarteret med tvåtillståndsceller som, även om de inte motiveras av fysiska överväganden, leder till intressant dynamik.
Småkryp
I "Critters"-regeln vänder övergångsfunktionen tillståndet för varje cell i ett block, förutom ett block med exakt två levande celler som förblir oförändrat. Dessutom genomgår block med tre levande celler en 180-graders rotation samt tillståndsomkastningen. Detta är en reversibel regel, och den följer bevarandelagar om antalet partiklar (att räkna en partikel som en levande cell i jämna faser och som en död cell i udda faser) och om pariteten för antalet partiklar längs diagonala linjer. Eftersom det är reversibelt förblir initiala tillstånd där alla celler tar slumpmässigt valda tillstånd ostrukturerade under hela utvecklingen. Men när den startas med ett mindre fält av slumpmässiga celler centrerat inom ett större område av döda celler, leder denna regel till komplex dynamik liknande den i Conways Game of Life där många små mönster som liknar livets glidflygplan flyr från det centrala slumpmässiga området och interagera med varandra. Till skillnad från segelflygplanen i Life, innebär reversibilitet och bevarandet av partiklar tillsammans att när segelflygplan kraschar ihop i Critters, måste åtminstone en fly, och ofta tillåter dessa krascher båda inkommande segelflygplan att rekonstruera sig själva på olika utgående spår. Med hjälp av sådana kollisioner kan denna regel också simulera biljardbollsmodellen för beräkningar, om än på ett mer komplext sätt än BBM-regeln. Critters-regeln kan också stödja mer komplexa rymdskepp med varierande hastighet samt oscillatorer med oändligt många olika perioder.
tron
I "Tron"-regeln lämnar övergångsfunktionen varje block oförändrat förutom när alla fyra av dess celler har samma tillstånd, i vilket fall deras tillstånd är omvända. Att köra denna regel från initiala förhållanden i form av en rektangel av levande celler, eller från liknande enkla rakkantade former, leder till komplexa rätlinjiga mönster. Toffoli och Margolus föreslår också att den här regeln kan användas för att implementera en lokal synkroniseringsregel som gör det möjligt att simulera vilken cellulär automat i Margolus-kvarter som helst med hjälp av en asynkron cellulär automat . I denna simulering lagrar varje cell i en asynkron automat både ett tillstånd för den simulerade automaten och en andra bit som representerar pariteten för en tidsstämpel för den cellen; därför har den resulterande asynkrona automaten dubbelt så många tillstånd som automaten den simulerar. Tidsstämplarna är begränsade till att skilja sig med högst en mellan intilliggande celler, och varje block med fyra celler vars tidsstämplar alla har korrekt paritet kan uppdateras enligt den blockregel som simuleras. När en uppdatering av denna typ utförs, bör tidsstämpelspariteterna också uppdateras enligt Tron-regeln, som nödvändigtvis bevarar begränsningen för intilliggande tidsstämplar. Genom att utföra lokala uppdateringar på detta sätt är utvecklingen av varje cell i den asynkrona automaten identisk med dess utveckling i den synkrona blockautomaten som simuleras.
Se även
- Tandpetarsekvens , ett fraktalt mönster som kan emuleras av cellulära automater med Margolus-kvarteret
externa länkar
- Critters simulation , Seth Koehler, Univ. av Florida