Balanspussel

En animering av en lösning på problemet med ett falskt mynt som involverar tio mynt. I det här exemplet är det falska myntet lättare än de andra.

Ett balanspussel eller vägningspussel är ett logiskt pussel om att balansera föremål – ofta mynt – för att avgöra vilka som har ett annat värde, genom att använda balansvågar ett begränsat antal gånger. Dessa skiljer sig från pussel som tilldelar föremål vikt, genom att endast den relativa massan av dessa föremål är relevant.

Känd	Mål	Maximalt antal mynt för $n$ vägningar	Antal vägningar för $c$ -mynt
Om målmynt är lättare eller tyngre än andra	Identifiera mynt	$3^{n}$	$\lceil \log _{3}(c)\rceil$
Målmynt skiljer sig från andra	Identifiera mynt	${\frac {3^{n}-1}{2}}$	$\lceil \log _{3}(2c+1)\rceil$
Målmynt skiljer sig från andra, eller så är alla mynt lika	Identifiera om det finns ett unikt mynt och om det är lättare eller tyngre	${\frac {3^{n}-1}{2}}-1$	$\lceil \log _{3}(2c+3)\rceil$

Till exempel, vid detektering av ett olikt mynt i tre vägningar (n = 3), är det maximala antalet mynt som kan analyseras 3 ³ − 1 / 2 = 13. Observera att med 3 väger och 13 mynt är det inte alltid möjligt för att fastställa identiteten på det sista myntet (om det är tyngre eller lättare än resten), utan bara att myntet är annorlunda. I allmänhet, med n väger, kan du bestämma identiteten på ett mynt om du har 3 ⁿ − 1 / 2 - 1 eller färre mynt. I fallet n = 3 kan du verkligen upptäcka identiteten på det olika myntet av 12 mynt.

Problem med nio mynt

Lösning på balanspusslet för 9 mynt i 2 vägningar, där det udda myntet är lättare än de andra – om det udda myntet var tyngre än de andra, byts de två övre grenarna i varje vägningsbeslut

Ett välkänt exempel har upp till nio föremål, säg mynt (eller kulor), som är identiska i vikt förutom en, som är lättare än de andra - en förfalskning (en udda kula). Skillnaden är märkbar endast genom att väga dem på en våg — men endast mynten i sig kan vägas. Hur kan man isolera det förfalskade myntet med bara två vägningar?

Lösning

För att hitta en lösning överväger vi först det maximala antalet föremål från vilka man kan hitta den lättare på bara en vägning. Det maximala antalet är tre. För att hitta det lättare kan vi jämföra två valfria mynt och utelämna det tredje. Om de två mynten väger lika mycket, måste det lättare myntet vara ett av dem som inte finns på vågen. Annars är det den som indikeras som lättare av vågen.

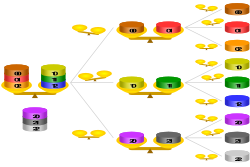
Föreställ dig nu de nio mynten i tre högar med tre mynt vardera. I ett drag kan vi hitta vilken av de tre stackarna som är lättare (dvs. den som innehåller det ljusare myntet). Det tar sedan bara ett drag till för att identifiera ljusmyntet inifrån den lättare stapeln. Så i två vägningar kan vi hitta ett enkelt lätt mynt från en uppsättning av $3 \times 3 = 9$ .

I förlängningen skulle det bara ta tre vägningar för att hitta det udda lätta myntet bland 27 mynt, och fyra vägningar för att hitta det från 81 mynt.

Tolvmyntsproblem

En mer komplex version har tolv mynt, varav elva eller tolv är identiska. Om en är annorlunda vet vi inte om den är tyngre eller lättare än de andra. Den här gången kan balansen användas tre gånger för att avgöra om det finns ett unikt mynt - och om det finns, för att isolera det och bestämma dess vikt i förhållande till de andra. (Detta pussel och dess lösning dök upp första gången i en artikel 1945.) Problemet har en enklare variant med tre mynt i två vägningar, och en mer komplex variant med 39 mynt i fyra vägningar.

Lösning

Detta problem har mer än en lösning. Man är lätt skalbar till ett högre antal mynt genom att använda bas-tre-numrering: märka varje mynt med ett annat nummer med tre siffror i bas tre, och placera vid n-te väga alla mynt som är märkta med n - te siffra identisk med skyltens etikett (med tre skyltar, en på varje sida av skalan märkt 0 och 2, och en utanför skalan märkt 1). Andra steg-för-steg-procedurer liknar följande. Det är mindre okomplicerat för detta problem, och den andra och tredje vägningen beror på vad som har hänt tidigare, även om så inte behöver vara fallet (se nedan).

Fyra mynt läggs på varje sida. Det finns två möjligheter:

1. Den ena sidan är tyngre än den andra. Om så är fallet, ta bort tre mynt från den tyngre sidan, flytta tre mynt från den lättare sidan till den tyngre sidan och placera tre mynt som inte vägdes första gången på den lättare sidan. (Kom ihåg vilka mynt som är vilka.) Det finns tre möjligheter:

1.a) Samma sida som var tyngre första gången är fortfarande tyngre. Det betyder att antingen myntet som stannade där är tyngre eller att myntet som stannade på den lättare sidan är lättare. Att balansera ett av dessa mot ett av de andra tio mynten avslöjar vilket av dessa som är sant, vilket löser pusslet.

1.b) Den sida som var tyngre första gången är lättare andra gången. Det betyder att ett av de tre mynten som gick från den lättare sidan till den tyngre sidan är det lätta myntet. För det tredje försöket, väg två av dessa mynt mot varandra: om ett är lättare är det det unika myntet; om de balanserar är det tredje myntet det lätta.

1.c) Båda sidor är jämna. Det betyder att ett av de tre mynten som togs bort från den tyngre sidan är det tunga myntet. För det tredje försöket, väg två av dessa mynt mot varandra: om ett är tyngre är det det unika myntet; om de balanserar är det tredje myntet det tunga.

2. Båda sidor är jämna. Om så är fallet är alla åtta mynten identiska och kan läggas åt sidan. Ta de fyra återstående mynten och placera tre på ena sidan av vågen. Placera 3 av de 8 identiska mynten på andra sidan. Det finns tre möjligheter:

2.a) De tre återstående mynten är lättare. I det här fallet vet du nu att ett av dessa tre mynt är det udda och att det är lättare. Ta två av dessa tre mynt och väg dem mot varandra. Om balansen tippar är det lättare myntet det udda myntet. Om de två mynten balanserar är det tredje myntet som inte finns på balansen det udda ut och det är lättare.

2.b) De tre återstående mynten är tyngre. I det här fallet vet du nu att ett av dessa tre mynt är det udda och att det är tyngre. Ta två av dessa tre mynt och väg dem mot varandra. Om balansen tippar är det tyngre myntet det udda ut. Om de två mynten balanserar så är det tredje myntet som inte finns på balansen det udda ut och det är tyngre.

2.c) De tre återstående mynten balanserar. I det här fallet behöver du bara väga det återstående myntet mot något av de andra 11 mynten och detta talar om för dig om det är tyngre, lättare eller likadant.

Variationer

Med en population på 13 mynt där det är känt att 1 av de 13 skiljer sig (massan) från resten, är det enkelt att avgöra vilket mynt det är med en balans och 3 tester enligt följande:

1) Dela in mynten i 2 grupper om 4 mynt och en tredje grupp med de återstående 5 mynten.

2) Test 1, Testa de 2 grupperna med 4 mynt mot varandra:

a. Om mynten balanserar är det udda myntet i populationen av 5 och fortsätt till test 2a.

b. Det udda myntet finns bland befolkningen på 8 mynt, fortsätt på samma sätt som i 12 myntsproblemet.

3) Test 2a, testa 3 av mynten från gruppen med 5 mynt mot valfria 3 mynt från populationen av 8 mynt:

a. Om de 3 mynten balanserar, är det udda myntet bland den återstående populationen av 2 mynt. Testa ett av de 2 mynten mot något annat mynt; om de balanserar är det udda myntet det sista oprövade myntet, om de inte balanserar är det udda myntet det aktuella testmyntet.

b. Om de 3 mynten inte balanserar, är det udda myntet från denna population av 3 mynt. Var uppmärksam på balanssvingens riktning (upp betyder att det udda myntet är lätt, nedåt betyder att det är tungt). Ta bort ett av de 3 mynten, flytta ett annat till andra sidan av balansen (ta bort alla andra mynt från balansen). Om saldot jämnar ut är det udda myntet det mynt som togs bort. Om balansen växlar riktning är det udda myntet det som flyttades till andra sidan, annars är det udda myntet det mynt som förblev på plats.

Med ett referensmynt

Om det finns ett äkta mynt som referens kan de misstänkta mynten vara tretton. Numrera mynten från 1 till 13 och det autentiska myntnumret 0 och utför dessa vägningar i valfri ordning:

0, 1, 4, 5, 6 mot 7, 10, 11, 12, 13
0, 2, 4, 10, 11 mot 5, 8, 9, 12, 13
0, 3, 8, 10, 12 mot 6, 7, 9, 11, 13

Om vågen bara är ur balans en gång, måste det vara ett av mynten 1, 2, 3 — som bara förekommer i en vägning. Om det aldrig blir balans så måste det vara ett av mynten 10–13 som förekommer i alla vägningar. Att välja ut det förfalskade myntet som motsvarar vart och ett av de 27 utfallen är alltid möjligt (13 mynt ett antingen för tungt eller för lätt är 26 möjligheter) förutom när alla vägningar är balanserade, i vilket fall det inte finns något falskt mynt (eller dess vikt är korrekt). Om mynten 0 och 13 tas bort från dessa vägningar ger de en generisk lösning på problemet med 12 mynt.

Om två mynt är förfalskade, väljer denna procedur i allmänhet inte någon av dessa, utan snarare något autentiskt mynt. Till exempel, om både mynt 1 och 2 är förfalskade, är antingen mynt 4 eller 5 felaktigt plockade.

Utan referensmynt

I en avslappnad variant av detta pussel behöver man bara hitta det falska myntet utan att nödvändigtvis kunna säga dess vikt i förhållande till de andra. I det här fallet kan helt klart vilken lösning som helst som tidigare vägde varje mynt någon gång anpassas för att hantera ett extra mynt. Detta mynt läggs aldrig på vågen, men om alla vägningar är balanserade väljs det ut som det förfalskade myntet. Det går inte att göra bättre, eftersom vilket mynt som helst som någon gång läggs på vågen och plockas ut som det falska myntet då alltid kan tilldelas vikt i förhållande till de andra.

En metod som väger samma uppsättningar mynt oavsett utfall låter en heller

(bland 12 mynt A–L) dra slutsatsen om de alla väger lika mycket, eller hitta det udda myntet och berätta om det är lättare eller tyngre, eller
(bland 13 mynt A–M) hitta det udda myntet och, med 12/13 sannolikhet, säg om det är lättare eller tyngre (för den återstående 1/13 sannolikheten, bara att det är annorlunda).

De tre möjliga utfallen av varje vägning kan betecknas med "\" för att vänster sida är lättare, "/" för att höger sida är lättare och "–" för båda sidor som har samma vikt. Symbolerna för vägningarna är listade i följd. Till exempel betyder "//–" att den högra sidan är lättare vid första och andra vägningen, och båda sidorna väger lika mycket vid den tredje vägningen. Tre vägningar ger följande 3 ³ = 27 utfall. Förutom "–––" är uppsättningarna uppdelade så att varje uppsättning till höger har ett "/" där uppsättningen till vänster har ett "\", och vice versa:

/// \\\ \// /\\ /\/ \/\ //\ \\/ \/– /\– –\/ –/\ /–\ \–/ \\– //– –\ \ –// \–\ /–/ /–– \–– –/– –\– ––/ ––\ –––

Eftersom varje vägning endast ger ett meningsfullt resultat när antalet mynt på vänster sida är lika med antalet på höger sida, bortser vi från den första raden, så att varje kolumn har samma antal "\" och "/"-symboler (fyra av varje). Raderna är märkta, ordningen på mynten är irrelevant:

\// A lätt /\\ A tung /\/ B lätt \/\ B tung //\ C lätt \\/ C tung \/– D lätt /\– D tung –\/ E lätt –/\ E tung /–\ F lätt \–/ F tung \\– G lätt //– G tung –\\ H lätt –// H tung \–\ I lätt /–/ I tung /–– J lätt \–– J tung –/– K lätt –\– K tung ––/ L lätt ––\ L tung ––– M antingen lättare eller tyngre (13-myntsfodral), eller så väger alla mynt samma (12-myntsfodral)

Med hjälp av mönstret av utfall ovan kan sammansättningen av mynt för varje vägning bestämmas; till exempel antyder uppsättningen "\/– D ljus" att mynt D måste vara på vänster sida vid den första vägningen (för att den sidan ska bli lättare), på höger sida på den andra och oanvänd i den tredje:

1:a vägning: vänster sida: ADGI, höger sida: BCFJ 2:a vägning: vänster sida: BEGH, höger sida: ACDK 3:e vägning: vänster sida: CFHI, höger sida: ABEL

Resultaten läses sedan av bordet. Till exempel, om den högra sidan är lättare i de två första vägningarna och båda sidorna väger lika i den tredje, innebär motsvarande kod "//– G tung" att myntet G är det udda och det är tyngre än de andra .

Generaliseringar

Generaliseringen av detta problem beskrivs i Chudnov.

Låt $\mathbb {R} ^{n}$ vara det $n$ -dimensionella euklidiska rummet , $[\mathrm {e} ^{1}, \mathrm {e} ^{2}]$ vara den inre produkten av vektorerna $\mathrm {e} ^{1}$ och $\mathrm {e} ^{2}$ från $\mathbb {R} ^{n},$ För vektorer $\mathrm {e} =(e_{1},\dots , e_{n})\in \mathbb {R} ^{n}$ och delmängder $E=\{\mathrm {e} ^{j}\}\subseteq \ mathbb {R} ^{n},$ operationerna $(\cdot )^{*}$ och $(\cdot )^{+}$ definieras, respektive, som $\mathrm {e} ^{*}=(tecken(e_{i}))_{i}$ ; $E^{*}=\{(\mathrm {e} ^{j})^{*}\}$ , $\mathrm {e} ^{+}=(|tecken(e_{i})|)_{i}$ , $E^{+}=\{(\mathrm {e} ^{j})^{+}\}.$ Med $I^{n}$ ska vi beteckna den diskreta [−1 ; 1]-kub i $\mathbb {R} ^{n}$ ; dvs mängden av alla sekvenser av längd $n$ över alfabetet $I=\{-1,0,1\}$ Mängden $I_{t}^{n}=\{\mathrm {x} \in I^{n}|w(\mathrm {x} )\leq t\} \subseteq I^{n}$ är den diskreta kulan med radien $t$ (i Hamming-metriken $w()$ ) med centrum i punkten $\mathrm {0} .$ Relativ vikt för $n$ objekt ges av en vektor $\mathrm {x} =( x_{1},\dots ,x_{n})\in I^{n},$ som definierar konfigurationerna av vikterna för objekten: ${\displaystyle i}:$ e objektet har standardvikt om $x_{i}=0;$ vikten av ${\displaystyle i}:$ e objektet är större (mindre) med ett konstant (okänt) värde om $x_{i}=1$ (respektive $x_{i}=-1$ ). Vektorn $\mathrm {x} ^{+}$ karakteriserar typerna av objekt: standardtypen, den icke-standardiserade typen (dvs. konfigurationer av typer), och den innehåller inte information om relativa vikter av icke-standardiserade objekt.

En vägning (en kontroll) ges av en vektor $\mathrm {h} \in I^{n};$ resultatet av en vägning för en situation $\mathrm {x} \in I^{n}$ är ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=tecken([\mathrm {x} ;\mathrm {h} ]).} Vägningen som ges av en$ vektor $\mathrm {h} =(h_{1},\dots ,h_{n})$ har följande tolkning: för en given kontroll deltar ${\displaystyle i}:$ e objektet i vägningen om $h_{i}\neq 0$ ; den läggs på den vänstra vågskålen om $h_{i}<0$ och läggs på den högra behållaren om $h_{i}>0.$ För varje vägning $\mathrm {h}$ , båda panorerna bör innehålla samma antal objekt: om antalet objekt på någon panorering är mindre än vad det borde vara, så får det några $r(\mathrm {h} )=[\mathrm {h} ;1,\dots ,1]$ referensobjekt. Resultatet av en vägning $s(\mathrm {x} ;\mathrm {h} )$ beskriver följande fall: balansen om $s(\ mathrm {x} ;\mathrm {h} )=0$ , vänster panorering uppväger den högra om $s(\mathrm {x} ;\mathrm {h} )= -1$ , och den högra panoreringen uppväger den vänstra om $s(\mathrm {x} ;\mathrm {h} )=1.$ Den ofullständiga initiala informationen om fördelning av vikter för en grupp av objekt kännetecknas av mängden tillåtna fördelningar av vikter av objekt $Z\subseteq I^{n},$ som också kallas uppsättningen av tillåtna situationer, elementen av $z\in Z$ kallas tillåtna situationer.

Varje vägning $\mathrm {h}$ inducerar uppdelningen av mängden $I^{n}$ av planet ( hyperplan ) $[\mathrm {x} ;\mathrm {h} ]=0$ i tre delar $W(s|I^{n};\mathrm {h} )=\{\mathrm {x} \in I^{n}|s(\mathrm {x } ;\mathrm {h} )=s\}$ , $s\in I,$ och definierar motsvarande partition för mängden $Z=W(0|Z,\mathrm {h} )+W(1|Z,\mathrm {h} )+W(-1| Z,\mathrm {h} ),$ där $W(s|Z,\mathrm {h} )=W(s|I^{n},\mathrm {h} )\cap Z.$

Definition 1 . En vägningsalgoritm (WA) ${\mathcal {A}}$ med längden $m$ är en sekvens ${\mathcal {A} }=<\mathrm {A} _{1},\dots ,\mathrm {A} _{m}>,$ där $\mathrm {A} _{j }:I^{j-1}\to I^{n}$ är funktionen som bestämmer kontrollen $\mathrm {h} ^{j}=\mathrm {A} _{j}(s^{j-1});\mathrm {h} ^{j}\in I ^{n},$ vid varje ${\displaystyle j}:$ e steget, $j=1,2,\dots ,m,$ av algoritmen från resultaten av $\mathrm {s} ^{j-1}=(s_{1},\dots ,s_{j-1} )\in I^{j-1}$ vägningar vid de föregående stegen ( $\mathrm {h} ^{1}=\mathrm {A} _{1}()$ är en given första kontroll).

Låt $S(Z,{\mathcal {A}})$ vara mängden av alla $(Z,{\mathcal {A}})$ -syndrom och $W(s|{\mathcal {A}})\subseteq I$ är uppsättningen av situationer med samma syndrom $s$ ; dvs $W(s|{\mathcal {A}})=\{\mathrm {z} \in I^{m}|s(z|{\mathcal {A} })=s\}$ ; $W(s|Z;{\mathcal {A}})=W(s|{\mathcal {A}})\cap Z.$

Definition 2 . A WA ${\mathcal {A}}$ sägs: a) identifiera situationerna i en mängd $Z$ om villkoret $|W(s|Z,{\mathcal {A}})|=1$ är uppfylld för alla $s\in S(Z{\mathcal {A}});$ b) identifiera typerna av objekt i en uppsättning $Z$ om villkoret $|W^{+}(s|Z{\mathcal {A}})|=1$ är uppfylld för alla $s\in S(Z{\mathcal {A}}).$

Det är bevisat genom att för så kallade lämpliga uppsättningar $Z$ en identifieringsalgoritm identifierar typerna även situationerna i $Z.$

Som ett exempel konstrueras de perfekta dynamiska (två-kaskad) algoritmerna med parametrarna $n=11,m=5,t=2$ som motsvarar parametrarna för perfekt ternär Golay-kod (Virtakallio-Golay-kod). Samtidigt konstateras att en statisk WA (dvs viktningskod) med samma parametrar inte existerar.

Var och en av dessa algoritmer som använder 5 vägningar hittar bland 11 mynt upp till två förfalskade mynt som kan vara tyngre eller lättare än riktiga mynt med samma värde. I detta fall innehåller osäkerhetsdomänen (uppsättningen av tillåtna situationer) $1+2C_{11}^{1}+2^{2}C_{ 11}^{2}=3^{5}$ situationer, dvs den konstruerade WA ligger på Hamming-gränsen för $t=2$ och är i denna mening perfekt.

$n,t$ finns andra perfekta WA som identifierar situationerna i $I_{t}^{n}$ för vissa värden på . Dessutom är det inte känt om det för vissa $t>2$ finns lösningar för ekvationen ${\displaystyle \sum _{i=0}^{ t}2^{i}C_{n}^{i}=3^{m}} ($ motsvarande Hamming-gränsen för ternära koder) vilket uppenbarligen är nödvändigt för existensen av en perfekt WA. Det är bara känt att för $t=1$ finns det inga perfekta WA, och för $t=2$ har denna ekvation den unika icke-triviala lösningen ${\ displaystyle n=11,m=5}$ som bestämmer parametrarna för den konstruerade perfekta WA.

Original parallell vägningspussel

Eliran Sabag uppfann detta pussel{1https://www.youtube.com/watch?v=y7auJNBA0bs}. Det finns N oskiljbara mynt, varav ett är falskt (det är inte känt om det är tyngre eller lättare än de äkta mynten, som alla väger likadant). Det finns två balansvågar som kan användas parallellt. Varje vägning varar i tre minuter. Vilket är det största antalet mynt N som det är möjligt att hitta det falska myntet för på tio minuter?

I litteraturen

Niobe, huvudpersonen i Piers Anthonys roman With a Tangled Skein , måste lösa tolvmyntsvarianten av detta pussel för att hitta sin son i helvetet : Satan har förklät sonen för att se identisk ut med elva andra demoner, och han är tyngre eller lättare beroende på om han är förbannad att ljuga eller kan tala sanning. Lösningen i boken följer det givna exemplet 1.c.
Beremiz, huvudpersonen från Júlio César de Mello e Souzas bok The Man Who Counted möter en indisk köpman som utmanar honom med standardbalanspusslet med åtta identiskt formade pärlor (en pärla något ljusare än resten). Beremiz löser det genom att explicit rama in alla variabler i problemet, med bara två vägningar.

I tv

I avsnittet "The Wedding Scammer" av Cyberchase måste gruppen av huvudpersoner hitta en lättare nyckel av åtta nycklar (de andra sju väger lika mycket), och de löser det suboptimalt, med tre viktningar, när två räcker.
I avsnittet "The Bye-Bye Sky High IQ Murder Case" av Columbo löser Columbo följande pussel: https://www.mathsisfun.com/puzzles/weighing-10-bags-solution.html
I avsnittet "Captain Peralta" av Brooklyn Nine-Nine presenterar Holt för sitt team en version av problemet med tolv mynt som involverar tolv män och en gungbräda.

externa länkar